It is almost a stereotype to walk into a retirement home and see seniors playing bingo. However, thanks to COVID 19, the game enjoys an unexpected revival among young adults. This week I will play the game for a second time this year with approximately 50 colleagues, most of them logging in remotely from their homes.
The game
We will play bingo the classical way, drawing balls from a cage containing 75 balls, numbered 1 through 75. Each player has a bingo card containing 25 squares arranged in 5 rows and 5 columns labeled B-I-N-G-O. The square in the center of the grid is marked ‘free’, resulting in 24 unique numbers on the card. The objective of this post is to find out how many drawing are required to have a winner. The winner is the first player who completes all 24 numbers on his card.
What are the odds?
We start with a bingo cage containing N balls. We assume that each of n players receives one card containing K numbers generated from a random sample without replacement from the set {1…K}. In our case we have N=75 and K=24.
Let p(x) be the probability that it takes exactly x drawings to complete one bingo card:
(1) 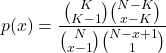
Let F(x) be the probability that it takes at the most x drawings to complete one bingo card:
(2) ![]()
Finally, let Fn(x) be the probability that it takes at the most x drawings to complete one out of n bingo cards:
(3) ![]()
Results
The results in the table below have been generated by this notebook. The mpmath library takes care of processing some very small probabilities with the adequate level of precision.
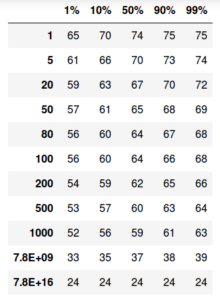
The table shows that when 50 players participate, the game is likely to take between 61 and 68 drawings from the bingo cage (80% confidence). It will be very likely (99% confidence) that a game will take at the most 69 drawings. It will be very unlikely (1% probability) that the game will be completed in less than 57 drawings.
What would happen if all world citizens (at the moment of writing 7.8 billion people) would participate in our bingo game? In that case, we would still have to wait between 33 and 39 bingo balls to be drawn till the first person will call out “Bingo!”. Even more amazing, each world citizen would have to participate with 10 million bingo cards in his hand to be (almost) certain that the first bingo occurs after 24 drawings from the bingo cage. Happy Bingo!
Acknowledgements: I would like to express my gratitude to Joey de Mol, data analytics consultant at Triple A, for his valuable contribution to this post.

